Конечно-разностный метод

«Рассмотрим первую краевую задачу:

{	y" + p(x)y' + q(x)y = f(x),  a < x < b;	(3.1)
	y(a) = ya,   x = a;	(3.2)
	y(b) = yb,   x = b	(3.3)

и будем решать ее конечно - разностным методом, заменяя дифференциальные операторы отношением конечных разностей с использованием формул численного дифференцирования.

Для этого введем конечно-разностную сетку с шагом h: ω _h = {x_i = ih, i = 0,...,n}.

Поскольку ОДУ (3.1) описывает поведение функции у(х) внутри расчетной области x ∈ (a,b) , то производные 1-го и 2-го порядков можно аппроксимировать с помощью отношения центральных разностей со 2-м порядком аппроксимации:

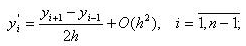	(3.4)
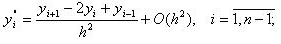	(3.5)
{p(xi), q(xi), f(xi)} ≡ {pi, qi, fi}, i= 1,...,n-1	(3.6)

Подставляя (3.4)-(3.6) в ОДУ (3.1), получим следующую конечно-разностную схему:

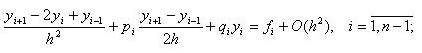
y₀ = y_a, i = 0; y_n = y_b, i = n, которую можно представить в виде следующей СЛАУ с трехдиагональной матрицей: a_i y_i-1 + b_i y_i + c_iy_i+1 = d_i,  i=1,...,n-1, (3.7)

где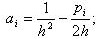

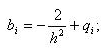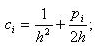di = fi.

При i = 1 первое слагаемое в левой части (3.7) известно и равно a₁y₀ = a₁y_a; при i = n-1 последнее слагаемое в левой части также известно и равно c_n-1y_n = c_n-1y_b. Поэтому СЛАУ (3.7) приобретает следующий вид:

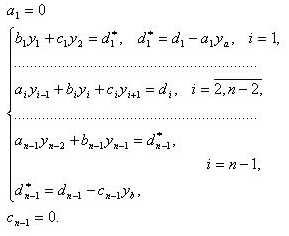(3.8)

Здесь коэффициенты a_i и c_n-1 полагаются равными нулю только после вычисления правых частей d₁^* и d_n-1^*.