Пример_2

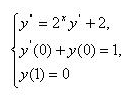
Решение:

Введем конечно - разностную сетку на отрезке [0,1] с шагом

h =	1 - 0	:  ω = 0,25	:   (рис. 3.1) :
	4

i	0	1	2	3	4
xi	0	0,25	0,5	0,75	1

Производные первого и второго порядков, входящие в дифференциальное уравнение, в узлах x_i, аппроксимируются со вторым порядком (3.17)-(3.18). Подставляя выражения (3.17)-(3.18) в дифференциальное уравнение для узлов x_i, i = 1,2,3, получим конечно – разностную аппроксимацию:

Так как на правой границе (i = 4, x₄ = 1) задано граничное условие первого рода, т.е. значение искомой функции в этом узле известно и равно y₄ = 0, то уравнение для этого узла не выписывается (но значение будет использовано в конечно - разностной аппроксимации при i = 3). Будем аппроксимировать со вторым порядком левое краевое условие в узле i = 0, x₀ =0.

Разложим на точном решении y₁ в ряд Тейлора в окрестности граничной точки x₀ = 0 до третьей производной включительно, получим:

Подставляя вместо y₀^" значение второй производной из заданного дифференциального уравнения при x₀ = 0 : y₀^" = 2^x₀ y₀^' + 2. Затем разделим все выражения на h и выразим из полученного равенства значение y₀^', получим:

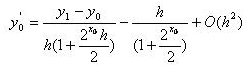
Подставим это выражение в левое краевое условие вместо производной первого порядка, получим:

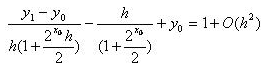
Откуда при x₀ = 0 и h = 0,25 получаем алгебраическое уравнение в узле x₀ = 0 со вторым порядком: -2,556y₀ + 3,556y₁ = 1,222 + O(0,0625)

Приписывая к этому уравнению алгебраические уравнения, полученные из (3.20) для i = 1, 2, 3, получим следующую СЛАУ с трехдиагональной матрицей:

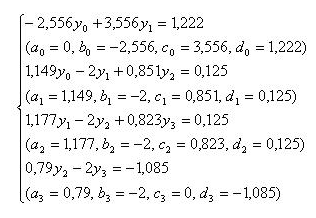
Решим полученную матрицу методом прогонки. Вычислим коэффициенты в среде Mathcad:

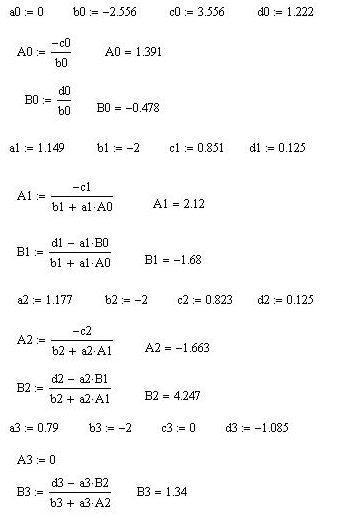
Рис. 3.2

Зная коэффициенты, найдем значения y_i.

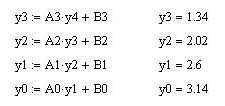
Рис. 3.3

Таким образом, результат можно представить в следующем виде: