краевых задач
метод
Конечно-разностный метод
Прогоночные коэффициенты в прямом ходе определяются с помощью выражений
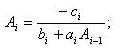
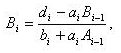
i=1,...,n-1,
(3.9)
Причем
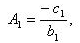
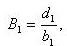
так как a1 = 0, An-1 = 0, так как cn-1 = 0.
Значения
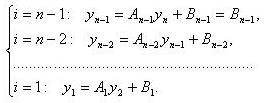 |
»[7, 176-178 c.] (3.10) |
«Рассмотрим вторую краевую задачу:
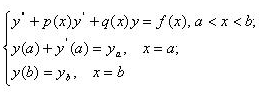 |
(3.11) (3.12) (3.13) |
Для этого введем конечно-разностную сетку «на отрезке [a,b] с шагом
| h = | b - a | : ωh = {xi = ih, i = 0, ... , n}. |
| n |
На этой сетке определяются сеточные функции
Фиксируя в уравнении (3.11)
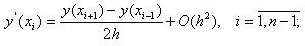 |
(3.17) |
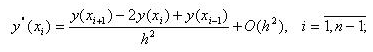 |
(3.18) |
В результате подстановки (3.17)-(3.18) в равенства (3.16) при i=1,2,… n-1 получаем (обозначения которых соответствуют (3.15)):
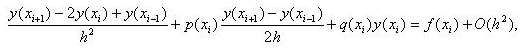 |
(3.19) |
После приведения подобных членов в (3.19) получаем стандартное трехточечное разностное уравнение второго порядка
| (1 + | h | pi) yi+1 - (2 - h2 qi) yi + (1 + | h | pi) yi-1 = h2 fi, где i = 1, 2,..., n-1 | (3.20) |
| 2 | 2 |
Интерпретируя (3.20) как компактную запись системы линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов, видим, что число уравнений в ней
Будем рассматривать два варианта аппроксимации входящих в краевые условия»[1, 626-628 c.].
«С этой целью разложим функцию на точном решении в ряд Тейлора до 3-й производной включительно в окрестности узла
Затем значения производных 2-го порядка для граничных узлов в этих разложениях заменяются значениями второй производной, определенными из ОДУ, после чего из полученных выражений определяются значения первой производной в граничных узлах со вторым порядком, которые затем подставляются вместо производных первого порядка в краевые условия.



| Карта сайта | | | Список литературы | | | Об авторе |