Конечно-разностный метод

Из (3.11) находим y₀^" : y₀^" = f₀ - p₀y₀^' - q₀ y₀. (3.22) Подставив (3.22) в (3.21) и разделив на h, получим

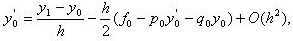
откуда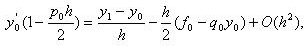

или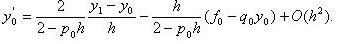

(3.23)

Подставляя (3.23) в краевое условие второго рода: y^'(a) + αy(a) = y_a, получим

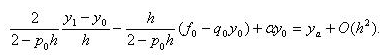(3.24)

Из (3.24) видно, что полученное уравнение для узла x₀ = aсодержит только два неизвестных y₀ и y₁, а аппроксимация имеет второй порядок. Следовательно (3.24) можно представить в виде b₀ y₀ +c₀ y₁ = d₀, (3.25)

где

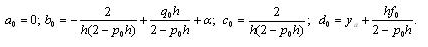
Аналогично для правой границы (x_n = b):

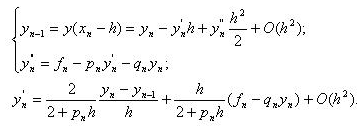
Подставляя это выражение в краевое условие y^'(b) + ß y(b) = y_b, получим уравнение для правой границы с двумя неизвестными y_n-1, y_n и вторым порядком аппроксимации:

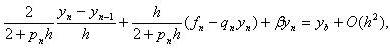
которое можно представить в виде a_ny_n-1 + b_ny_n = d_n, (3.26)

где

Таким образом, результирующая СЛАУ с трехдиагональной матрицей теперь будет содержать n + 1 уравнение, каждое из которых получено со вторым порядком точности, а именно: уравнение (3.25) при i = 0 , уравнения (3.20) для i = 1, ... , n-1 и уравнение (3.26) для i = n. Для ее решения используется метод прогонки, поскольку a₀ = 0 и c_n = 0»[7, 179-180 c.].

«Поэтому СЛАУ приобретает следующий вид:

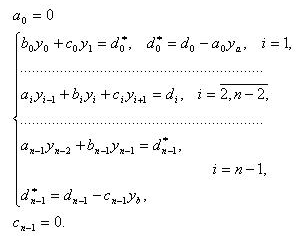(3.27)